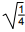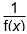Study Guide
Overview and Test Objectives
Field 022: Mathematics (Secondary)
Test Overview
| Format | Computer-based test (CBT) |
|---|---|
| Number of Questions | 80 multiple-choice questions |
| Time | 2 hours 30 minutes* |
| Passing Score | 220 |
*Does not include 15-minute CBT tutorial
Test Objectives
| Subarea | Range of Objectives | Approximate Percentage of Questions on Test | |
|---|---|---|---|
| 1 | Mathematical Processes and Number Concepts | 001–004 | 22% |
| 2 | Patterns, Algebraic Relationships, and Functions | 005–009 | 28% |
| 3 | Measurement and Geometry | 010–013 | 22% |
| 4 | Data Analysis, Statistics, Probability, and Discrete Mathematics | 014–018 | 28% |
Hover over each subarea for details of subtest content or see table above.
Sub area 1 22%, Sub area 2 28%, Sub area 3 22%, and Sub area 4 28%.
Subarea 1—MATHEMATICAL PROCESSES AND NUMBER CONCEPTS
Objective 001—Understand principles of mathematical reasoning and techniques for communicating mathematical ideas.
Includes:
- analyzing the nature and purpose of axiomatic systems
- using inductive and deductive logic to develop and validate conjectures
- applying the laws of deductive logic to draw valid conclusions
- developing counterexamples to a conjecture
- developing and evaluating direct and indirect proofs
- using appropriate mathematical terminology
- translating common language into symbols and vice versa
- using a variety of numeric, symbolic, and graphic methods to communicate mathematical ideas and concepts
- making connections among numeric, symbolic, graphic, and verbal representations
Objective 002—Understand problem-solving strategies, connections among different mathematical ideas, and the use of mathematics in other fields.
Includes:
- devising, carrying out, and evaluating a problem-solving plan
- applying a range of strategies (e.g., drawing a diagram, working backwards, creating a simpler problem) to solve problems
- analyzing problems that have multiple solutions
- selecting an appropriate tool or technology to solve a given problem
- recognizing connections among two or more mathematical concepts (e.g., Fibonacci numbers and the golden rectangle symmetry and group theory)
- exploring the relationship between geometry and algebra
- applying mathematics across the curriculum and in everyday contexts
Objective 003—Understand number systems and equivalent ways of representing numbers.
Includes:
- identifying characteristics and relationships among natural, whole, integer, rational, irrational, real, imaginary, and complex numbers (e.g., 1 half = 0.5 = 50% = square root of one fourth )
- applying properties of number operations (e.g., commutative, distributive)
- applying order relations to numbers
- using set operations (e.g., union, intersection, complement)
- using manipulatives, verbal expressions, and geometric models to represent numbers
Objective 004—Understand number theory and operations on number systems.
Includes:
- analyzing properties of prime numbers, factors, multiples, and divisibility
- extending the relationships of primes, factors, multiples, and divisibility in an algebraic setting
- using scientific notation to compute with very large and very small numbers
- comparing and contrasting models of operations across number systems (e.g., using a rectangular array to model multiplication of whole numbers and fractions)
- solving problems involving ratios and proportional reasoning
- using manipulatives, verbal expressions, and geometric models to represent number operations
- applying and evaluating estimation strategies
- analyzing standard and nonstandard computational algorithms
- solving a variety of problems using number operations
- performing operations with complex numbers (e.g., conjugates, products, roots)
- using rectangular, polar, matrix, and vector representations to solve problems
Subarea 2—PATTERNS, ALGEBRAIC RELATIONSHIPS, AND FUNCTIONS
Objective 005—Describe, analyze, and generalize mathematical patterns.
Includes:
- recognizing and extending numerical and geometric patterns
- constructing, representing, and recording patterns using charts, tables, graphs, matrices, and vectors
- exploring and describing symmetric and spatial patterns (e.g., fractals, tessellations)
- analyzing and generalizing sequences, series, and recursive patterns
- using patterns to make inferences, predictions, and decisions
Objective 006—Use symbolic expressions to describe and analyze patterns of change and functional relationships.
Includes:
- exploring patterns of change characteristic of families of functions (e.g., quadratic, exponential, periodic)
- translating among verbal, graphic, tabular, and symbolic representations of functions
- distinguishing between relations and functions
- analyzing functions in terms of range, domain, and intercepts
- exploring function operations [e.g., f(x) + g(x)], composition [e.g., f(g(x))], and inverses
- using piecewise- and recursively defined functions
- analyzing the relationship among the graphs of f(x) and transformations such as f(x ± c), cf(x), and 1 over f(x)
- using graphing calculators and utilities to analyze properties of functions
Objective 007—Understand properties and applications of linear and quadratic functions, and solve related equations and inequalities.
Includes:
- analyzing linear relationships
- modeling and solving problems using linear equations and inequalities
- investigating the relationship between a linear equation and its graph
- modeling and solving problems using linear systems (e.g., using matrices, using graphs)
- solving quadratic equations, inequalities, and systems using a variety of methods (e.g., graphical, analytic)
- using graphing calculators to solve systems of equations
- analyzing how changing the coefficients of a quadratic function changes its graph
- using quadratic functions to model and solve problems, including maximum and minimum problems
Objective 008—Understand properties and applications of polynomial, rational, radical, exponential, logarithmic, and trigonometric functions, and solve related equations and inequalities.
Includes:
- exploring the properties and graphs of polynomial, rational, radical, exponential, logarithmic, and trigonometric (i.e., sine, cosine, tangent) functions
- applying these functions to develop and evaluate models of real-world situations
- modeling and solving problems using polynomial, rational, radical, exponential, logarithmic, and trigonometric equations and inequalities
- analyzing the relationship between exponential and logarithmic functions
- examining the relationship between trigonometric functions and their inverses
- examining the relationship between trigonometric functions and circular functions
- modeling periodic phenomena using trigonometric functions
Objective 009—Understand principles and applications of differential and integral calculus.
Includes:
- investigating limits and limiting processes
- using limits to determine continuity
- analyzing the relationships among the graph, slope of the secant line, and the derivative of a function
- using differential calculus to analyze the graph of a function
- analyzing the relationship among the area under a curve, Riemann sums, and integration
- using the principles of calculus and appropriate technology to solve a variety of theoretical and applied problems
Subarea 3—MEASUREMENT AND GEOMETRY
Objective 010—Understand attributes of measurement and measuring units.
Includes:
- selecting appropriate units to estimate and record measurements of angle (degree and radian), length, area, volume, mass, temperature, and time
- identifying tools for performing measurements
- converting measurements within measurement systems
- analyzing how changes in the measurement of one attribute relate to changes in others
- using dimensional analysis to solve problems
- solving problems involving density, pressure, rates of change, and other derived units
- evaluating precision, accuracy, measurement errors, and percent error
Objective 011—Apply measurement principles to analyze the spatial characteristics of two- and three-dimensional shapes.
Includes:
- deriving and applying formulas for the perimeter, area, surface area, or volume of two- and three-dimensional composite figures
- exploring scale factors for the area and volume of similar figures
- applying right triangle trigonometry and the Pythagorean theorem to solve problems (e.g., problems involving indirect measurements)
- interpreting three-dimensional drawings of objects
- analyzing cross sections and nets of three-dimensional figures
Objective 012—Apply geometric principles of points, lines, angles, planes, congruence, and similarity to analyze the formal characteristics of two- and three-dimensional shapes.
Includes:
- determining necessary and sufficient conditions for the existence of a particular shape
- analyzing concepts (e.g., parallelism) in Euclidean and non-Euclidean geometries
- applying properties of parallel and perpendicular lines and angles to analyze shapes
- comparing and analyzing shapes and formally establishing the relationships among them (e.g., congruence, similarity)
- using geometric principles to prove theorems
- applying properties of two-dimensional shapes to analyze three-dimensional shapes
- recognizing the uses of dynamic geometry software in making conjectures and investigating properties of shapes
Objective 013—Apply properties of geometric transformations and coordinate and vector methods to describe geometric objects in two and three dimensions.
Includes:
- analyzing figures in terms of translations, reflections, rotations, dilations, and contractions
- applying transformations to explore the concepts of congruence and similarity
- using transformations to characterize the symmetry of an object
- representing transformations using matrices
- analyzing the composition and inverse of transformations
- describing the abstract algebraic properties of a set of transformations under composition
- locating objects in terms of their position using rectangular, polar, and three-dimensional coordinate systems
- locating and describing the locus of points that satisfy a given condition
- applying concepts of slope, distance, midpoint, and parallel and perpendicular lines to determine the geometric and algebraic properties of figures in the coordinate plane (including conic sections)
- describing the position and movement of objects using vectors
Subarea 4—DATA ANALYSIS, STATISTICS, PROBABILITY, AND DISCRETE MATHEMATICS
Objective 014—Understand methods of collecting, organizing, and displaying data.
Includes:
- formulating questions requiring data gathering and applying appropriate techniques for collecting data
- analyzing factors that may affect the validity of a survey, including bias
- organizing data using tables and spreadsheets
- creating a variety of charts to display data (e.g., pie charts, box plots, stem-and-leaf plots, scatter plots, frequency histograms)
- using appropriate technology to organize and display data
- evaluating the source, organization, and presentation of data
Objective 015—Understand methods of describing, analyzing, and interpreting data.
Includes:
- analyzing the shape, location, and spread of a data distribution using algebraic and geometric methods to estimate a variety of statistics
- describing the range and outlines of a set of data
- applying and interpreting measures of central tendency (e.g., mean, median, mode) and spread (e.g., range, standard deviation)
- analyzing the effects of data transformations on measures of central tendency and spread
- finding the function (e.g., linear, exponential, logarithmic) that best represents a set of data
- using appropriate technology to analyze and manipulate data
- evaluating the validity of statistical arguments
Objective 016—Understand methods of making predictions and inferences based on data.
Includes:
- analyzing and explaining data trends
- making and testing hypotheses
- using simulations and sampling to test inferences
- applying principles of interpolation and extrapolation
- analyzing linear regression lines and correlation coefficients
- analyzing the relationship between sample size and width of confidence interval
- employing confidence intervals in making predictions and inferences based on data
Objective 017—Understand the theory of probability and probability distributions.
Includes:
- enumerating the sample space of an event
- determining simple and compound probabilities
- finding the probability of dependent and independent events
- using simulations and sampling to determine experimental probabilities
- solving problems using geometric probability (e.g., ratio of two areas)
- applying probability distributions (e.g., binomial, normal) to solve problems
- modeling and solving real-world problems using probability concepts
Objective 018—Understand principles of discrete mathematics.
Includes:
- solving counting problems using permutations and combinations
- using sets and set relations to represent algebraic and geometric concepts
- using vertex-edge graphs to solve network problems such as finding circuits, critical paths, minimum spanning trees, and adjacency matrices
- proving statements using the principle of mathematical induction
- employing recursion and iteration methods to model problems
- describing and analyzing efficient algorithms to accomplish a task or solve a problem in a variety of contexts (e.g., practical and computer-related situations)
- using discrete mathematics concepts to model a problem, evaluate the existence of solutions, determine the number of possible solutions, and choose the optimal solution to the problem
- using linear programming to model and solve problems