Study Guide
Field 131: Mathematics (7–12)
Sample Multiple-Choice Questions
Expand All Answers | Collapse All Answers
The following reference material will be available to you during the test:
Subarea 1—Pedagogical Knowledge and Practices for Teaching Mathematics
Objective 001—Promote Equitable Teaching
1. A teacher's lesson plan has three instructional activities. First, the teacher will demonstrate how to solve a two-step linear equation in one variable. Next, the teacher will solve three sample problems with the class, and then students will complete two problems on their own. Which of the following strategies would best encourage student participation?
- The teacher displays two worked-out student solutions for each problem on a whiteboard in front of the class and provides students with time to compare their work with the displayed solutions. Students raise their hand if they have a question about the solutions.
- The teacher randomly selects students by drawing from a collection of craft sticks with student names on them. Those students then explain how they found a solution for one problem and ask the class whether they agree or disagree with their solution.
- The teacher gives students the correct solutions and then has students raise their hand if they got both answers correct. The teacher then selects a student who answered both questions correctly to explain the solutions.
- The teacher groups students in pairs. One student in each pair develops a solution, and the other student interprets the solution and describes the strategy used by the first student.
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: D.
Objective 002—Plan for Effective Instruction
2. A teacher sets a goal of measuring how well students understand each day's learning target in order to adapt instruction before introducing new content. Which of the following assessment strategies best supports this goal?
- concluding the lesson with an exit ticket that contains a mathematical exercise related to the topic studied that day
- using polling software to survey how well each student believes they understood that day's lesson on a scale of low, medium, and high
- creating a warm-up activity for the next day in which the teacher can observe students discussing the topic from the previous day's lesson
- assigning students an unscheduled quiz that contains at least one conceptual question and one procedural question about the mathematics studied in that day's lesson on the following day
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Objective 003—Implement Effective Instruction
3. A ninth-grade teacher assigns a task on graphing lines in standard form. Most students graph the lines after first converting the lines to slope-intercept form. Few students graph the lines by finding both the x- and y-intercepts. The teacher reflects on the activity and plans to make changes for future lessons. Which of the following changes will most effectively encourage students to make use of characteristics of lines in standard form when graphing?
- investing more instructional time in developing the concepts of x- and y-intercepts and the connections to standard form
- revising the task so that the lines presented are difficult to graph in slope-intercept form because of fractional values
- displaying a graphic organizer in the room that describes effective ways to graph lines in different forms
- shifting instructional emphasis to set standard form as a default and teaching slope-intercept afterward
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Objective 004—Enhance Teaching Through Collaboration with Colleagues, Families, and Community
4. An eighth-grade teacher wants to develop a collaborative partnership with parents/guardians by providing them with information about their children's progress. The students are currently working through their first unit of study and the teacher wants to ensure that they are as prepared as possible for their first summative assessment. Which of the following strategies would best meet the teacher's goals?
- contacting each student's parent/guardian directly at least once during the first unit
- developing a checklist of skills that will be assessed on the summative assessment and sending this home with students
- maintaining an online record book that has descriptions of each assignment and updating this record with students' numerical grades daily
- having each student write a paragraph describing what they are learning and then sharing this with their parent/guardian at the end of each week
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Subarea 2—Students as Learners of Mathematics
Objective 005—Anticipate and Attend to Students' Thinking About Mathematics Content
5. A seventh-grade teacher provides an assignment for which students must apply facts about supplementary, complementary, and vertical angles to determine an unknown measurement in a geometric figure. Which of the following teacher actions represents the inclusion of a metacognitive learning strategy in this assignment?
- describing how this type of problem appears in the context of a real-world situation
- asking students to identify a step in their solution that they found challenging to complete
- presenting a correct response that students may use to determine whether their solution is accurate
- preparing additional problems that may be shared with students who find the original problem to be too easy or too difficult
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: B.
Objective 006—Promote Students' Engagement in Mathematical Practices
6. A tenth-grade student factors the expression 12 X squared plus 23 X plus 10 by creating the binomials the binomial X plus question mark times the binomial 12 X plus question mark. The student attempts to use a guess-and-check method to complete the factorization. The student becomes frustrated because they cannot find two constants that complete the factorization. The teacher can best support the student's ability to analyze the structure of trinomials of this form by asking which of the following questions?
- "Could you use factors other than 1 and 12 to get the coefficient of X squared?"
- "How does a prime coefficient like 23 affect the factorization of a polynomial?"
- "What do you notice about the trinomial produced by multiplying the binomial A X plus B times the binomial C X plus D?"
- "How could solutions from the equation 12 X squared plus 23 X plus 10 equals 0 help you factor the expression?"
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Objective 007—Cultivate Positive Mathematical Identities of Students
7. At the start of the school year, a teacher plans to have students review several solutions to a warm-up question. At least one of the work samples contains an error that leads to an incorrect answer. Which of the following statements by the teacher would most effectively encourage students to consider the analysis of these various solutions as an opportunity for learning?
- "Let's consider each work sample and attempt to infer what the author was thinking when they made their mistake."
- "Each of the students worked diligently to create these answers, so let's all pay attention and learn from their work."
- "Let's watch for errors and misconceptions in each solution so that you may avoid making them yourself."
- "As we review the work samples, let's consider the strengths of the different approaches."
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: D.
Subarea 3—Understanding of Social Contexts of Mathematics Teaching and Learning
Objective 008—Provide Access and Opportunity
8. A county announces that there will be a math competition, open to all students, where students will compete to answer mathematical problems. The winners of the competition will earn a scholarship to a summer math camp. Which of the following strategies can a teacher use to best promote broad access to the county competition?
- integrating problems similar to those from the competition into classwork and then encouraging students to compete once they discover that they can solve those types of problems
- surveying students to gauge their interest in participating in the competition and then providing support to students who are interested
- creating an assessment that will be used to determine which students in the class should participate in the competition
- selecting the students with the highest math grades and meeting with them during lunch to prepare for the competition
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Objective 009—Understand Power and Privilege in the History of Mathematics Education
9. Which of the following instructional practices inhibits equitable, high-quality learning opportunities for students?
- requiring students to include writings or drawings to explain their mathematical ideas
- providing some students with more assistance than others to complete learning activities
- introducing mathematical problems without context (i.e., using numbers and equations only) to present ideas in a universal format
- instructing students to practice describing mathematical relationships using precise mathematical language in addition to informal, everyday language
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: C.
Objective 010—Enact Ethical Practices for Advocacy
10. Toward the end of a school year, a teacher's eighth-grade students have the option of selecting their ninth-grade algebra classes. All classes cover a common curriculum, but some classes include additional content that prepares students to study advanced mathematics in their final two years of high school. The teacher is concerned that their students, many of whom are from traditionally marginalized groups, may be reluctant to select the more challenging courses because they may undervalue their own capabilities. Which of the following actions can the teacher use to best support students' access to advanced mathematics courses?
- sending a list of the students in the class to the high school with recommendations for the placement of each student
- reviewing data with each student regarding evidence that indicates their potential for success in more challenging courses
- providing students with high-quality resources to use to seek out knowledge of advanced mathematics outside of their high school classes
- inviting the high school mathematics department chair to the class to explain the sequence and scope of the available math courses in high school
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: B.
Subarea 4—Know Relevant Mathematical Content
Objective 011—Understand Essential Concepts in Number
11. A teacher presents the following theorem to a precalculus class.
Conjugate Pairs Theorem: Let F of X be a polynomial whose coefficients are real numbers. If R equals A plus B I is a zero of f, then the complex conjugate R bar equals A minus B I is also a zero of f.
The learning objective of the lesson is to determine the unknown zeros of a polynomial function. This theorem can be applied to which of the following factored polynomials to determine the unknown roots p and q?
- F of X equals the quantity X minus 2 times the quantity X minus 2 I times the quantity X plus 4 I times the quantity X minus P times the quantity X minus Q
- F of X equals the quantity X minus 2 times the quantity X plus 2 I times the quantity X minus 4 times the quantity X minus P times the quantity X minus Q
- F of X equals the quantity X minus 2 times the quantity X plus 2 times the quantity X plus 4 I times the quantity X minus P times the quantity X minus Q
- F of X equals the quantity X minus 2 times the quantity X minus 2 I times the quantity X minus 4 times the quantity X minus P times the quantity X minus Q
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Objective 012—Understand Essential Concepts in Ratios and Proportional Relationships
12. A seventh-grade teacher assigns an exit slip for which students write a sentence about how the equations Y equals 2 X and Y equals 2 X plus 8 are similar. Which of the following student responses best indicates an understanding of lines of the form Y equals K X and Y equals K X plus B?
- "The graphs of both equations must pass through the origin."
- "Both equations can be determined from a single point on their line."
- "Both equations increase by a constant rate of 2 as x increases by 1."
- "For both equations, any two unique coordinate points are proportional."
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: C.
Objective 013—Understand Essential Concepts in Algebra at a Comprehensive, Robust Level
13. A pair of tenth-grade students work to solve the equation X squared plus 6 X minus 2 equals 0.
Student A: That doesn't factor … Let's add 2 to both sides to get X squared plus 6 X equals 2 and then complete the square by adding 9 to both sides.
Student B: Wait, how did you know to add 9?
Student A: I don't know why, but you take half the coefficient of x and square it. That's the rule.
Which of the following algebraic products can the teacher use to justify this step in completing the square?
-
the quantity X plus A times the quantity X minus A
is equal to X squared plus A X minus A X minus A squared
which is equal to X squared minus A squared -
the quantity X plus A squared
is equal to X squared plus A X plus A X plus A squared
which is equal to X squared plus 2 A X plus A squared -
the quantity X plus A times the quantity X plus B
is equal to X squared plus A X plus B X plus A B
which is equal to X squared plus the quantity A plus B times X plus A B -
the quantity X plus A times the quantity X minus B
is equal to X squared plus A X minus B X minus A B
which is equal to X squared plus the quantity A minus B times X minus A B
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: B.
Objective 014—Understand Essential Concepts in Functions at a Comprehensive, Robust Level (e.g., Linear, Exponential, Polynomial, Absolute Value, Piecewise-Defined, Trigonometric, Logarithmic)
14. Students in a high school math class regularly use journals to respond to writing prompts that the teacher asks during a lesson. A teacher presents the following graph to students during a lesson about identifying key features of graphs of functions.
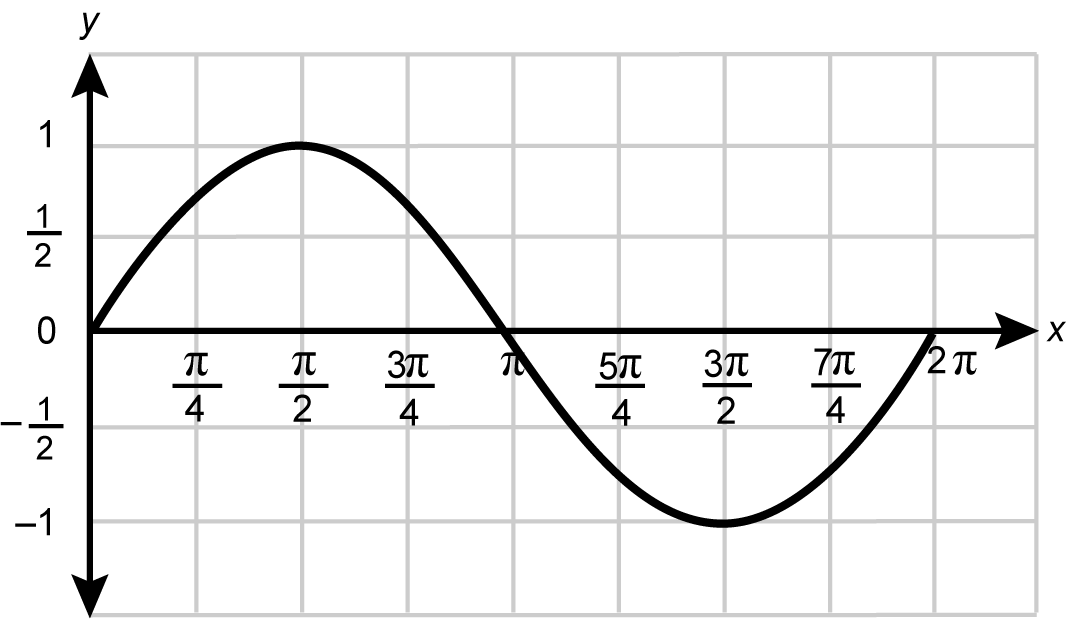
A graph of y = sine of x is shown on the interval from x equals 0 to x equals 2 pi.
Which of the following writing prompts should the teacher present to students to assess their ability to distinguish between a value of a function and the rate at which a function changes?
- Compare the properties of the graph at X equals 0 and X equals 2 pi.
- Compare the properties of the graph at X equals pi over 4 and X equals 3 pi over 4.
- Explain what the expressions F of 2 pi minus F of 0 and 2 pi minus 0 represent in the context of the graph.
- Explain what the expressions F of 3 pi over 2 minus F of pi over 2 and 3 pi over 2 minus pi over 2 represent in the context of the graph.
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: B.
Objective 015—Understand Essential Concepts in Statistics and Probability
15. A teacher introduces the concept of margin of error by presenting the information shown.
A survey reported that 74 percent of U S adults are completely satisfied or somewhat satisfied with the quality of their home Internet services. The results are based on telephone interviews with a random sample of 254 adults. The margin of error is plus or minus 8 percent.
Which of the following statements should the teacher use to explain the concept of margin of error?
- "Between 66 percent and 82 percent of the adults are completely satisfied or somewhat satisfied with the quality of their home Internet services."
- "There is an 8 percent likelihood that 74 percent of the population of adults would respond that they are completely satisfied or somewhat satisfied with the quality of their home Internet services."
- "There is a high plausibility that the actual percentage of adults who are completely satisfied or somewhat satisfied with the quality of their home Internet services is between 66 percent and 82 percent."
- "To account for possible mistakes in the data, the researchers calculated the number of adults who are completely satisfied or somewhat satisfied with the quality of their home Internet services to be in the interval of 66 percent to 82 percent."
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: C.
Objective 016—Understand Essential Concepts in Geometry, Trigonometry, and Measurement
16. A geometry teacher facilitates an activity in which students use a ruler to divide a square by choosing any arbitrary point along one side and naming the two segments a and b. Students then mark points that divide each of the other sides into segments of length a and b and connect the points to create a smaller square. The teacher calls students' attention to the areas of both squares.
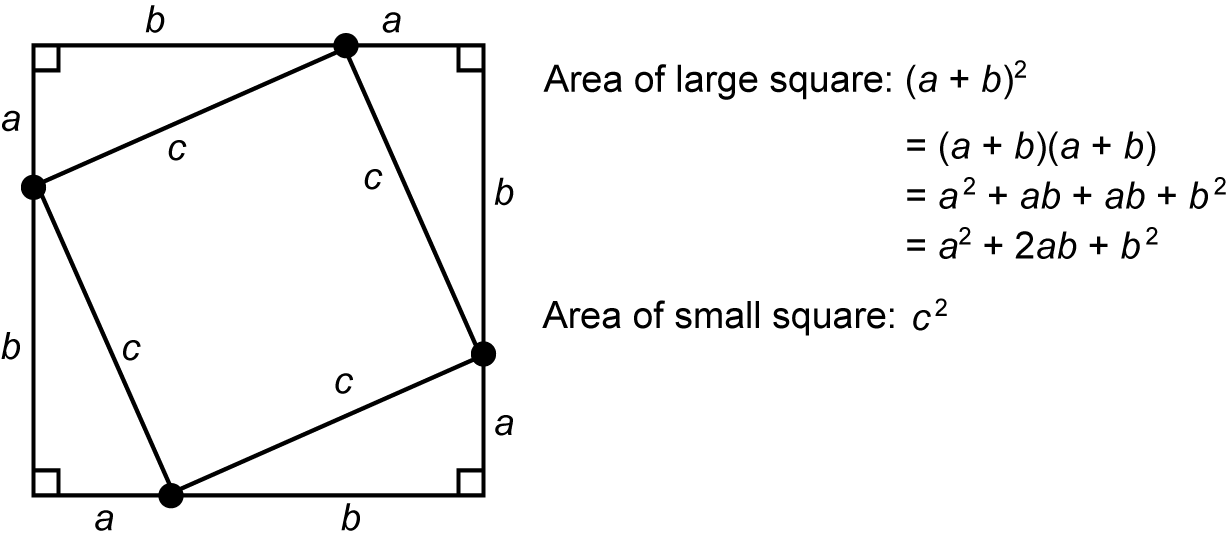
A partial proof of the Pythagorean Theorem is shown in which a square with side lengths c is inscribed within a larger square with side lengths (a + b) such that four right triangles are created with side lengths a, b, and c.
There is text to the right of the diagram that reads:
Area of the large square: a plus b the quantity squared, which equals the quantity a plus b times the quantity a plus b which equals a squared plus a b plus a b plus b squared which equals a squared plus 2 a b plus b squared.
There is another line of text below the previous line that reads:
Area of the small square: c squared.
The teacher can guide students to complete a proof of the Pythagorean theorem by asking them to complete which of the following steps?
- calculating the length of a diagonal in the smaller square
- repeating the process of dividing the sides to create smaller squares
- comparing the area of the four triangles to the area of the small square
- comparing the area of the small square to the area of the large square minus the area of the four triangles
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: D.
Objective 017—Understand Essential Concepts in Calculus at a Comprehensive, Robust Level (e.g., Linear, Exponential, Polynomial, Absolute Value, Piecewise-Defined, Trigonometric, Logarithmic)
17. A calculus teacher presents the following graph to the class using dynamic graphing software that displays the slope of the line containing points A and B.
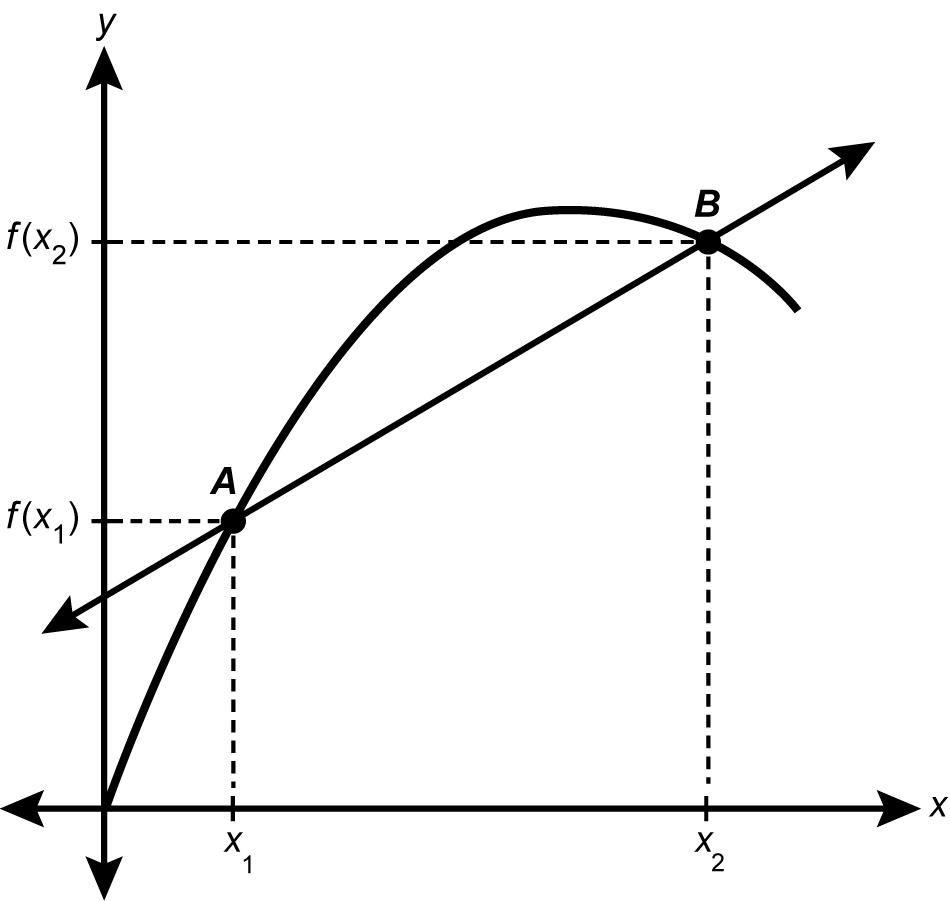
A parabolic curve is shown in the first quadrant of the coordinate plane with a y intercept of 0 and an absolute maximum at some positive x value.
Two points are indicated on the graph of the curve: Point A is located at the coordinates x sub 1, f of x sub 1, and Point B is located farther to the right on the curve at x sub 2, f of x sub 2. Dashed lines show the horizontal and vertical distance from points A and B to the x and y axes. The locations x sub 1 and x sub 2 are shown on the x axis, and the locations f of x sub 1 and f of x sub 2 are shown on the y axis. A line is drawn passing through the points A and B.
The teacher can best illustrate the concept of the derivative at X sub 1 by observing the slope value while clicking and dragging:
- point B to the left until X sub 2 equals X sub 1.
- point A to the right until F of X sub 1 equals F of X sub 2.
- point B to the maximum of the function.
- points A and B to the endpoints of the function.
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Objective 018—Understand Essential Concepts in Discrete Mathematics at a Comprehensive, Robust Level
18. A teacher presents an introductory lesson about recurrence relations. Which of the following limitations should the teacher discuss with students to support their ability to compare functions and recurrence relations?
- Recursive equations are not convenient to use when calculating distant terms in the sequence by hand (e.g., the twentieth term).
- Recursive reasoning can only be applied when the first and second terms of the sequence are known.
- Recursive equations are not useful for proving a statement by using mathematical induction.
- Recursive reasoning can only be applied to arithmetic and geometric sequences.
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Subarea 5—Mathematics Practices, Dispositions, Curriculum
Objective 019—Demonstrate Mathematical Practices
19. A teacher instructs students to respond to the following task in their math journals:
Let a be a rational number. Consider whether it is always, sometimes, or never true that the absolute value of A equals A and explain your reasoning.
Which of the following excerpts of student work best demonstrates the mathematical practice of attending to precision?
- "… the absolute value of A equals A means that A equals A or A equals negative A …"
- "… taking away the negative from negative 1 makes 1 …"
- "… it's as if there is a mirror between the left and right at 0 …"
- "… if a is 1 you get 1, if a is 2 you get 2, if a is 2.5 you get 2.5 …"
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: A.
Objective 020—Exhibit Productive Mathematical Dispositions
20. A ninth-grade teacher tells a class, "Math problems are solved in many different ways. Looking for new methods to solve problems is a fantastic way to learn mathematics." The teacher then presents the following problem.
- 40 percent of the students in a school play a musical instrument.
- 60 percent of the students in the school are in ninth grade.
- 25 percent of the students play an instrument and are in ninth grade.
What is the probability that a student in the school does not play an instrument or is in ninth grade?
One of the students asks whether they could begin the problem by assuming that the school has 1000 students. Which of the following teacher responses most effectively uses the student's thinking to reinforce the teacher's original statement about learning mathematics?
- "Let's consider the formula P of A plus P of B minus P of A and B. Where does 1000 belong in this formula?"
- "We could start with 1000, as you suggested, but can you think of an easier number to work with instead?"
- "Let's consider how your 1000 students distribute into the three categories. What are 40 percent, 60 percent, and 25 percent of 1000?"
- "The values that we are given are all percentages. Let's begin with these values first and then we can determine how 1000 students would be distributed."
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: C.
Objective 021—Analyze the Mathematical Content of Curriculum
21. The math teachers for grades 7 and 8 will begin a new textbook series at the start of the school year. The teachers know that some parents/guardians may wonder how these new textbooks will affect how students learn mathematics. The teachers develop a video for parents/guardians to watch about the new textbooks. Which of the following teacher strategies would best help parents/guardians support their child's transition to the new textbooks?
- explaining why the old textbooks needed to be replaced
- comparing how the new and old textbooks present similar topics
- describing how the new textbooks align to the district pacing guide
- presenting claims about students' depth of understanding with the new textbooks
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: B.
Objective 022—Use Mathematical Tools and Technology
22. In which of the following learning situations would physical manipulatives be more effective than virtual manipulatives?
- computing the volume of a cone by integrating disks
- investigating the relationship between the net of a cone and its volume
- applying the shell method of integration to derive the formula for the volume of a cone
- investigating the relationship between the volume of a cone and a cylinder of equal radius and height
- Answer. Enter to expand or collapse. Answer expanded
- Correct Response: D.