Skip to main content

Study Guide

Field 117–120: Lower Elementary (PK–3) Education
Subtest 3: Mathematics
Sample Multiple-Choice Questions

Expand All Answers | Collapse All Answers

Subarea 1—Mathematics-Specific Teaching Practices

Objective 001—Build and draw on relationships with children, caregivers, and communities in ways that support children's mathematics learning.

1. A kindergarten teacher observes as a small group of students practice comparing numbers and quantities using manipulatives. Each student has four counters. One student's counters are spaced farther apart than the other students' counters, and several members of the group claim that student has more counters than everyone else. The teacher can build on the students' understanding of counting and cardinality by:

  1. encouraging the one student to count their counters for the group.
  2. identifying the error and moving the one student's counters closer together.
  3. asking probing questions about the total number of counters each student has.
  4. prompting the group to combine their counters and count how many they have in all.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
  1. Having one student count their own set of counters aloud does not address the misconception that the number of counters in a set depends on how they are arranged.
  2. This manner of addressing the misconception does not necessarily build upon the students' understanding because the teacher did not check whether they grasped the explanation or provide them with opportunities to explain in their own words why the total number of objects in each group is the same.
  3. Correct. By asking probing questions about the total number of counters each student has, the teacher can help students move beyond a naïve conception that bigger equals more and deepen their conceptual understanding of counting and cardinality.
  4. The affordances created by combining the counters into a large group do not offer these students more substantive insights into understanding counting and cardinality concepts than the affordances created by using smaller groups of counters.
Objective 002—Plan mathematics lessons and sequences of lessons.

2. A first-grade teacher plans initial lessons on comparing number values. Which of the following activities would be developmentally appropriate and engaging when introducing this concept?

  1. Students form multiple-digit numbers using index cards labeled with the digits 1, 2, 3, and 4.
  2. Students measure the lengths of classmates' shoes and then sort the shoes from smallest to largest.
  3. Students discuss the values of different piles of coins, such as a pile of 5 quarters and a pile of 5 pennies.
  4. Students stand between two different quantities and arrange their arms into a greater-than or less-than symbol.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.
  1. This activity does not require students to compare numbers.
  2. The skills required to measure and sort rational numbers—the numbers that would be used to describe shoe lengths—are too advanced to be included in a first-grade lesson activity about comparing number values.
  3. This activity is not developmentally appropriate because the concepts of number comparison should be introduced to students without requiring them to also apply additional mathematical knowledge that does not directly support their understanding of these concepts.
  4. Correct. The alignment and rigor of the activity is developmentally appropriate for introducing first-grade students to the concept of comparing number values and the kinesthetic activity promotes their engagement.
Objective 003—Use formative and summative mathematics assessments to gauge children's learning and to make instructional decisions.

3. First-grade students consider the following equations.

7 = 10 − 3
7 = 5 + 2
10 − 3 = 5 + 2

Most students state that the last equation is incorrect. In order to address the students' misconception, the teacher should plan a review of which of the following concepts?

  1. meaning and function of the equal sign
  2. how addition and subtraction are related
  3. the use of benchmark equations to find the answer
  4. the concepts of "greater than," "less than," and "equal to"
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.
  1. Correct. The teacher should review the meaning and function of the equal sign because students who agree that only the first two equations are correct may be interpreting the equal sign to be a symbol that indicates the result of the last operation (i.e., they would likely believe that the third equation should be written as 10 − 3 = 7 + 2 or 10 − 7 = 5 + 2).
  2. None of the equations shown makes use of addition and subtraction as inverse operations.
  3. A review of benchmark equations (e.g., sums and differences involving 5 and 10) is not necessary because students have previously agreed that 7 = 10 − 3 and 7 = 5 + 2.
  4. There is evidence that the students are interpreting "=" to mean "the result of the last operation," and reviewing the concepts of "greater than" and "less than" would not address this misconception directly or efficiently.
Objective 004—Enact instruction that allows all children to engage with significant mathematics and to develop productive dispositions toward mathematics.

4. A first-grade teacher uses an activity involving dice to help students make the jump from counting to addition. Students roll two dice, then determine the sum of the dots that are face up. On a piece of paper, students draw their dice as an addition problem and write the problem using numbers. One student's work is shown.

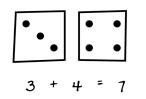
two dice

Two dice are shown above an equation. The left die shows 3 pips, the right die shows 4 pips, and the equation reads 3 plus 4 equals 7.

The teacher can increase students' success by taking which of the following actions before explaining the activity?

  1. teaching students how to add without using a counting strategy
  2. providing context by describing games in which dice may be used
  3. giving students the opportunity to become familiar with dice and their dots
  4. posting addition tables at the front of the room and on each student's desk
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
  1. Students should explore the relationship between counting and addition before they learn to add without a counting strategy.
  2. Describing games in which dice may be used does not direct students' attention to attributes of dice that makes them useful manipulatives for learning addition: the neat arrangement of dots on the faces, the unique numbers of dots on each side, and the many different outcomes that can be formed by rolling two dice.
  3. Correct. Providing students with opportunities to explore manipulatives on their own stimulates their curiosity, interest, and comfort with them and prepares students to explore how they may be used as mathematical tools.
  4. Posting addition tables does not support students' ability to understand how the mathematical concepts used to count a single collection of objects can be extended to count two combined collections of objects through addition.

Subarea 2—Mathematical Knowledge for Teaching Grades PK–3: Attribution and Counting and Whole Number Representation

Objective 005—Unpack mathematical content and identify mathematical competence for attribution.

5. The dramatic play area of a prekindergarten classroom is set up a like a kitchen, with three-dimensional blocks standing in for plates and cups. While children work in stations pretending to make and serve food to each other, the teacher can help the children extend their understanding of three-dimensional attributes by asking them:

  1. to find the yellow cup.
  2. which plate is their favorite.
  3. to bring a certain object to the table.
  4. how the plate and the cup are the same and different.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.
  1. The color yellow and the object name "cup" are not used to describe attributes of three-dimensional shapes.
  2. This question does not direct students to focus on the three-dimensional attributes of different plates.
  3. The name of an object is not a three-dimensional attribute.
  4. Correct. Students answer this question by describing the similarities and differences of the three-dimensional attributes of the plate and the cup (e.g., "The plate is short and flat, and the cup is tall", "The plate and the cup both have round edges").
Objective 006—Perform mathematical explanations and support children's mathematical explanations for attribution.

6. A teacher shares this geometric pattern with the class.

geometric shapes arranged in a row

A pattern formed from geometric shapes arranged in a row is shown. The shapes, from left to right, are a triangle, a square, a pentagon, a hexagon, a triangle, and a square.

The teacher asks students to explain the order of the shapes in the pattern. As students share their explanations, the teacher writes these student explanations on the board.

By writing these explanations on the board, the teacher:

  1. highlights the most efficient ways to explain the geometric pattern.
  2. encourages students to revise their explanations if they misinterpreted the pattern.
  3. offers students an entry point for collaboratively refining explanations of the geometric pattern.
  4. allows students to recognize explanations that are accurate and dismiss inaccurate explanations.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
  1. The teacher conducts the conversation about the pattern in a way that solicits a wide range of input from students without commenting about whether one description is more efficient than another.
  2. All students—not only those who misinterpreted the pattern—may wish to revise their explanations when they consider the other students' responses.
  3. Correct. By recording a wide range of student responses, the teacher exposes students to a rich variety of word choices and mathematical details that students can draw upon to refine their own explanation of the pattern.
  4. Dismissing students' responses creates a counterproductive learning dynamic, and while students may judge details in the responses to be accurate or inaccurate, the teacher is not likely recording the responses with the intention of having the students identify which should be removed.
Objective 007—Choose, interpret, and talk with representations for attribution.

7. A teacher considers using the image shown of a hanger to represent an example of triangles in the real world.

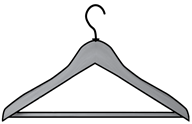
diagram of a flat wooden hanger

A flat wooden hanger is shown. The part of the hanger that attaches to the hook is flat on the bottom and has a varying thickness along its top. This part is arranged like an upside-down v, and the arms of this shape extend past a flat bar that attaches to it to provide horizontal support. An isosceles triangle appears along edges facing the interior of the hanger.

Which of the following statements best explains why a hanger is not a good example of a triangle?

  1. Not all triangles are isosceles.
  2. Not all triangles are made of wood.
  3. Students may not have schema for a hanger.
  4. The exterior of the hanger is not composed of straight lines.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.
  1. This explanation is not sufficient because it implies that the teacher must find a triangle that can represent all triangles, and such a triangle does not exist.
  2. The material used to create a triangle is not one of its defining attributes, and students should be exposed to triangles constructed out of a variety of materials, including wood, so they can understand why this true.
  3. Students should be presented with examples of real-world objects and situations that relate to the mathematics they are studying, regardless of whether they have been exposed to them before.
  4. Correct. A triangle has three straight sides, and this picture may introduce the misconception that a triangle may have curvy lines or rounded corners.
Objective 008—Elicit, interpret, support, and extend others' mathematical thinking for attribution.

8. Two students play in the block area. One student builds a tower using five blocks. A second student tries to build a similar tower with the same type of blocks, but it keeps falling over. The teacher hears the students have the following conversation.

Student A: You have to put this kind on the bottom. It's the biggest one.

Student B: No, this one is the biggest.

Student A: Not the biggest this way, the biggest that way.

The teacher wants to facilitate the students' thinking and language about shapes. Which of the following questions should the teacher use to achieve this goal?

  1. "What can you do to help your friend?"
  2. "Do you know how many sides your block has?"
  3. "Do you mean the base block needs to be bigger?"
  4. "Can you show or tell your friend how the block is bigger?"
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.
  1. This question is vague and does not help facilitate the students' discussion.
  2. The students are discussing an attribute of the block that does not depend on its number of sides.
  3. With this question, the teacher clarifies that the block can be called the "base block," but this information does not help students establish a common understanding of the attribute they are discussing.
  4. Correct. This question helps students establish a common understanding about how the word "biggest" applies to the shape.
Objective 009—Unpack mathematical content and identify mathematical competence for counting and whole number representation.

9. A teacher introduces a paired activity involving index cards that the teacher has numbered from 0 through 9. For the activity, the teacher gives each pair of students a set of index cards. Each student draws two cards, and together they use the numerals on the cards to make 2 two-digit numbers. They determine which of the two numbers is greater, recording their thinking as an inequality. Then, the students build both numbers using base-ten blocks to check if their thinking is correct. An appropriate learning target for this activity is for students to be able to:

  1. identify reasonable numbers as solutions.
  2. compare two numbers using place values.
  3. use mathematical tools to explain their thinking.
  4. construct numbers to solve mathematics problems.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.
  1. The students check their work by modeling the numbers with base-ten blocks and not by determining whether the numbers are reasonable solutions.
  2. Correct. Students compare numbers when they record their thinking as an inequality, and they use place values concepts to create representations of two-digit numbers to check their work.
  3. The use of mathematical tools in this activity, such as the use of base-ten blocks, supports students' understanding of the learning target but is not the learning target itself.
  4. This learning target does not specify the types of mathematics problems that are solved in this learning activity.
Objective 010—Perform mathematical explanations and support children's mathematical explanations for counting and whole number representation.

10. During a lesson on subtraction within 20, first-grade students engage with a series of word problems about lost items (e.g., books, toys, mittens). Some students have difficulty solving the subtraction problems without drawing out the entire scenario. The teacher can support these students as they think about subtraction by:

  1. encouraging the students to try a count-back or a count-up strategy.
  2. explaining how to use context to determine which operation to use.
  3. reminding the students of their prior learning regarding operations.
  4. explaining how addition and subtraction are related operations.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.
  1. Correct. Students who consistently solve subtraction problems by drawing (i.e., by creating lines or pictures to represent objects and then crossing them out) should be encouraged to practice other subtraction strategies, such as counting-back or counting-up, to promote their conceptual and procedural understanding.
  2. The students demonstrate that they know to use subtraction, so an explanation about determining an operation from a situational context is not necessary.
  3. This response does not specifically target students' demonstrated need to practice subtraction strategies that do not involve drawing them out.
  4. An explanation of how subtraction and addition are related operations (e.g., by explaining how the equations a − c = b and a + b = c are related) does not directly guide the students to apply subtraction strategies that do not require drawing.
Objective 011—Choose, interpret, and talk with representations for counting and whole number representation.

11. First-grade students play with tiles. One table group counts their tiles and finds there are 24. The teacher asks the students if they can group the tiles so they can identify the total number easily. A student creates the following representation:

diagram of an arrangement of 24 squares

A diagram of an arrangement of 24 squares is shown. The squares are positioned in rows. There are 10 squares in each of the first two rows and 4 squares in the third row.

Presenting this representation to the class demonstrates the use of manipulatives to:

  1. critique the reasoning of others.
  2. support reasoning with evidence.
  3. create a basis for the concept of grouping.
  4. develop understanding of the base-ten system.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.
  1. Opportunities for the class to engage in the constructive criticism of a student's reasoning, such as by participating in a discussion about the student's thought processes or suggesting possible refinements to their representation, have not taken place at this point in the learning activity.
  2. The student's reasons for grouping the tiles as shown have not yet been shared with the class.
  3. The ones unit is the only unit represented in the representation (i.e., each tile represents 1), and the basis of grouping, where a collection of 10 ones may be interchanged with a single unit of ten, is not illustrated here.
  4. Correct. The student arranged their representation for easy counting by forming two rows of 10 and one row of 4, and presenting this to the class helps them develop their understanding of the base-ten system.
Objective 012—Elicit, interpret, support, and extend others' mathematical thinking for counting and whole number representation.

12. First-grade students explore representations of two-digit numbers using base-ten blocks. The teacher asks one student to show the number 33. The student presents the following arrangement.

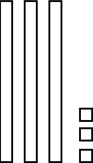
base-ten blocks arranged to show the number 33

The number 33 is shown represented with base-ten blocks. There are three ten-rods and three unit squares in this diagram.

When asked to explain their answer, the student says, "I know I need three of both since it's 3 and 3." Which of the following questions should the teacher ask to facilitate a clearer understanding of composing numbers greater than 10?

  1. "How would you explain the difference between a rod and a block?"
  2. "How would you show a number like 44 with rods and blocks?"
  3. "How can you use tally marks to represent the number 33?"
  4. "How can you explain the role of 3 in 333?"
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.
  1. Correct. This question helps to clarify whether the student interprets rods and blocks to represent different positions in the number (i.e., the left 3 means the number of rods and the right 3 means the number of blocks) or different units (i.e., the left 3 means 30, which is represented by 3 rods, and the right 3 means 3, which is represented by 3 blocks).
  2. The student would likely answer this question by saying, "I know I need four of both since it's 4 and 4," which doesn't offer any deeper insight into the student's thinking than the original answer.
  3. The student demonstrates at least a partial understanding of how to represent 33 with base-ten blocks, and the teacher should attempt to build upon the student's response rather than switch to a different representation—especially when the alternative representation does not demonstrate place-value concepts effectively.
  4. Expanding the number of place value positions is unlikely to help the student explain what value each digit of 3 represents.

Subarea 3—Mathematical Knowledge for Teaching Grades PK–3: Early Fraction Representation and Whole Number Operation

Objective 013—Unpack mathematical content and identify mathematical competence for early fraction representation.

13. An elementary school teacher places a pitcher of water on a table in the classroom. The teacher then initiates this discussion:

Teacher: How could this water be shared between 4 people equally?

Student A: You could pour it into 4 cups.

Student B: You should measure it, though.

Teacher: Why should you measure it?

Student B: To make sure everyone gets the same amount.

Teacher: So, the idea is to measure the water and split it into 4 cups, with everyone getting an equal amount.

By restating the students' thinking, the teacher can:

  1. motivate them to explore measurement skills independently.
  2. challenge connections they make between measurement and fractions.
  3. identify the mathematical competency they demonstrate in their approach.
  4. prompt them to engage in higher-level questioning during mathematics discussions.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
  1. The teacher restates the students' ideas to clarify their conversation, not to promote different measurement skills.
  2. The teacher's summary does not emphasize reasoning with fractions.
  3. Correct. The teacher can point out the students' mathematical understanding of the situation by restating their thinking.
  4. The teacher restates the students' thinking to focus on the points they have discussed, not to raise higher-level questions.
Objective 014—Perform mathematical explanations and support others' mathematical explanations for early fraction representation.

14. A third-grade teacher asks students how they would determine which fraction is greater when the fractions have the same numerator and a different denominator, like the fractions 2 thirds and 2 sixths, initiating the following conversation:

Student A: If you score two goals out of three attempts in soccer, that's better than two out of six. So 2 thirds is greater than 2 sixths.

Student B: But you still only scored two goals.

Student A: Yeah, but you scored more of the goals you attempted.

Which of the following interpretations best compares both students' explanations?

  1. Student A explains that a fraction is greater if the numerator is closer to the denominator, while Student B interprets only the denominator.
  2. Student A compares the fractions using a common number of attempts, while Student B compares only the number of goals scored.
  3. Student A uses equivalent fractions to compare magnitudes, while Student B compares the numerators as parts of the same whole.
  4. Student A interprets the number of attempts as the whole, while Student B compares only the number of goals scored.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: D.
  1. Student B does not consider the denominator when they interpret the fractions.
  2. Student A does not attempt to compare the two fractions by representing them with a common denominator.
  3. Student A does not use the concept of equivalent fractions in the discussion.
  4. Correct. Student A refers to the whole for each fraction when they say "three attempts" and "out of six," and Student B only compares the numerators when they say "only scored two goals."
Objective 015—Choose, interpret, and talk with representations for early fraction representation.

15. After a lesson on the progression of fractions from 0 to 1 using fourths, a teacher presents this problem to the class.

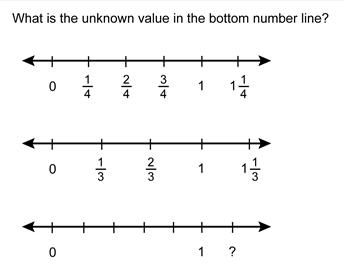
diagram of three number lines

A question is shown. It reads, "What is the unknown value in the bottom number line?"
Below this question, a diagram of three number lines is shown. The first number line displays the numbers 0, one-fourth, two-fourths, three-fourths, 1, and one and one-fourth.
The second number line shows 0, one-third, two-thirds, 1, and one and one-third.
The third number line shows 0, 1 and a question mark. The first tick mark is labeled 0, the fifth tick mark is labeled 1, and the sixth tick mark is labeled with a question mark.

One student responds, "The question mark is after the 1, so the answer is 1 and 1 half". Which of the following teacher responses would best prompt a discussion about unit fractions and iteration?

  1. "Which patterns do you notice between 0 and 1 in the first two number lines?"
  2. "Does the unknown mark on the number line look halfway between 1 and 2?"
  3. "Where does the fraction 1 half appear on the bottom number line?"
  4. "Should the missing value be greater or less than 1 and 1 third?"
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.
  1. Correct. This question encourages the student to make connections between the number of tick marks between 0 and 1 and the denominators of the fractions on the number line.
  2. The teacher would do better to assist the student with interpreting details that can be observed directly rather than by asking them to visualize features that are not present, such as visualizing where 2 would be if the number line were extended.
  3. The bottom number line is divided into fifths, which can make it difficult for the student to identify one-half when they demonstrate a misconception about how the tick marks relate to denominator of a fraction.
  4. This question does not address the student's misconception about the relationship between the tick marks in the number line and the denominator of a fraction.
Objective 016—Elicit, interpret, support, and extend others' mathematical thinking for early fraction representation.

16. A teacher assesses students' understanding of fractions with the following question on an exit slip:

Which fraction is greater: 3 fourths or 4 sixths?

A student responds that 4 sixths > 3 fourths and provides the following explanation.

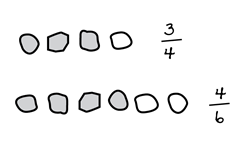
diagram of student work representing the fractions three-fourths and four-sixths

A diagram of student work representing the fractions three-fourths and four-sixths is shown.
Three-fourths is shown as three shaded parts and 1 unshaded part, with all parts arranged in a row. The fraction three-fourths is written to the right of this row.
Four-sixths is shown as four shaded parts and two unshaded parts, with all parts arranged in a row. The fraction four-sixths is written to the right of this row.
The two rows are vertically aligned and extend from left to right.

The student's response supports which of the following claims?

  1. The student understands that the value represented by the numerator depends on the value of the denominator.
  2. The student understands how to compare unit fractions with different denominators.
  3. The student understands how to interpret an individual fraction as a part of a whole.
  4. The student understands how to form different partitions of two equivalent wholes.
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
  1. The student's drawing shows evidence that they understand fractions as parts of a set and numerators as iterations of unit fractions, but this claim would only be supported if their drawing showed evidence that the unit fractions 1 fourth and 1 sixth were different, which it does not.
  2. For this to be true, the student would need to represent and compare 1 fourth and 1 sixth using a common whole; instead, they use unit fractions with equal sizes and then draw unequal wholes from them.
  3. Correct. The student's drawing accurately represents each fraction as parts of a whole, and this claim is not weakened or contradicted by the unequal sizes the student uses to represent the fraction wholes.
  4. The student does not show evidence of dividing the same whole into different amounts of equal parts (e.g., dividing a rectangle into fourths and dividing the same rectangle into sixths).
Objective 017—Unpack mathematical content and identify mathematical competence for whole number operations.

17. A teacher gives a small group of students a result-unknown word problem.

A farm has 12 chickens and 9 pigs. How many chickens and pigs are on the farm all together?

After the students arrive at the correct answer, the teacher asks a change-unknown word problem that builds on the information from the first word problem. Which of the following questions could be the question that the teacher asks?

  1. How many more chickens are on the farm than pigs?
  2. Each chicken lays one egg per day. How many total eggs are laid each day?
  3. Some ducks fly down to the farm. Now there are 25 animals on the farm. How many ducks are there?
  4. On the farm, 6 chickens run away. Then 5 more pigs join the farm. How many animals are there all together now?
Answer. Enter to expand or collapse. Answer expanded
Correct Response: C.
  1. This problem can be described by the result-unknown equation 12 − 9 = result unknown.
  2. This problem can be described with the result-unknown equation 12 × 1 = result unknown.
  3. Correct. This problem can be described by an equation where a change is unknown: 9 + 12 + unknown = 25 or 21 + unknown = 25.
  4. This problem can be described by the result-unknown equation (12 − 6) + (9 + 5) = result unknown.
Objective 018—Perform mathematical explanations and support children's mathematical explanations for whole number operations.

18. A teacher asks a student to solve the following problem.

Cup A contains 7 marbles. Cup B contains 3 marbles. How many more marbles are in Cup A than Cup B?

The student explains how they recognized it was subtraction because of the phrase "how many more." The student then shows their solution with a drawing. The student draws 7 marbles in Cup A and 3 marbles in Cup B. The student shades circles in Cup A until the cups match and then counts the shaded marbles to get an answer of 4.

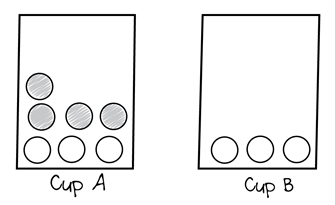
Two rectangles, each containing a number of circles

Two rectangles, each containing circles, is shown. The left rectangle is labeled Cup A. It contains 4 shaded circles and 3 unshaded circles. The right rectangle is labeled Cub B. it comes 3 unshaded circles.

The student's model is consistent with which of the following approaches?

  1. calculating a difference by comparison
  2. calculating a difference by adding or counting on
  3. calculating a difference by decomposing into anchor numbers
  4. calculating a difference by rewriting it as a more familiar expression
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.
  1. Correct. The student understands that "how many more" implies a difference, so they compared the number of marbles in Cup A to the number of marbles in Cup B by shading the greater set of marbles until both sets were equal.
  2. The student did not solve the problem by adding or counting on because they did not attempt to add marbles to Cup A until the quantities of marbles were equivalent.
  3. The student shows no evidence of decomposing either set of marbles into sums of different quantities, so this is not consistent with the student's solution.
  4. The student's solution is consistent with the subtraction problem as it was originally presented (i.e., 7 – 3) without rewriting it as a more familiar expression.
Objective 019—Choose, interpret, and talk with representations for whole number operations.

19. A third-grade teacher asks a student to solve 33 − 7 = ?, initiating the following conversation.

Student: The answer is 26.

Teacher: How did you get your answer?

Student: First, I took a 10 from 33, so I made it into 10 and 23. Then I took away 7 ones from the 10 and counted what was left to get 3 + 23, which is 26.

Teacher: Why did you make the 33 into 10 and 23?

Student: It was easier to subtract the 7.

Which of the following representations with base-ten blocks should the teacher use to model the student's approach?

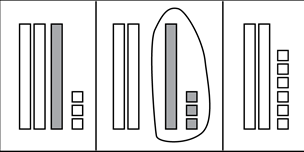
  1. a series of base-10 blocks being manipulated in 3 steps

    A diagram shows base-10 blocks being manipulated in 3 steps. The first step shows 2 unshaded rods, 1 shaded rod, and 3 unshaded squares. The second step shows 2 unshaded rods and 1 shaded rod and 3 shaded squares. The shaded rod and squares are circled. The third step shows 2 unshaded rods and 6 unshaded squares.

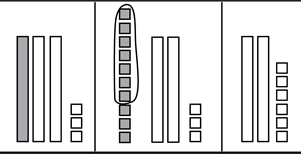
  2. a series of base-10 blocks being manipulated in 3 steps

    A diagram shows base-10 blocks being manipulated in 3 steps. The first step shows 1 shaded rod, 2 unshaded rods, and 3 unshaded squares. The second step shows 10 shaded square, 2 unshaded rods and 3 unshaded squares. Six of shaded squares are circled. The third step shows 2 unshaded rods and 6 unshaded squares.

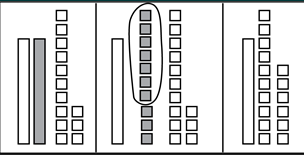
  3. a series of base-10 blocks being manipulated in 3 steps

    A diagram shows base-10 blocks being manipulated in 3 steps. The first step shows 1 unshaded rod and 1 shaded rod alongside 13 unshaded squares. The second step shows 1 unshaded rod, and 10 shaded squares, and 13 unshaded squares. Six of the shaded squares are circled. The third step shows 1 unshaded rod and 16 unshaded squares.

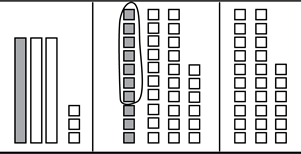
  4. a series of base-10 blocks being manipulated in 3 steps

    A diagram shows base-10 blocks being manipulated in 3 steps. The first step shows 1 shaded rod and 2 unshaded rods alongside 3 unshaded squares. The second step shows 10 shaded squares and 26 unshaded squares. Six of the shaded squares are circled. The third step shows 26 unshaded squares.

Answer. Enter to expand or collapse. Answer expanded
Correct Response: B.
  1. This representation shows the initial decomposition of 33 into 3 tens and 3 ones, its arrangement into a group of 2 tens and a group of 1 ten and 3 ones, and then the exchange of 1 ten and 3 ones for 6 ones; this does not model the student's description.
  2. Correct. This representation shows the decomposition of 33 into 3 tens and 3 ones, the grouping of 1 ten into 10 ones, and the removal of 7 ones from that group.
  3. This representation shows the decomposition of 33 into 2 tens and 13 ones, a regrouping of one 10 to create 1 ten and 23 ones, and then the removal of 7 ones; this does not match the student's description.
  4. This representation shows all the tens, an initial decomposition of 33 being traded for 30 ones, and then 7 ones removed from the 33 ones; this does not match the student's description.
Objective 020—Elicit, interpret, support, and extend others' mathematical thinking for whole number operations.

20. A first-grade student solves 8 + 5 and shows their work:

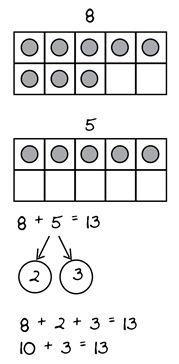
SHORT ALT TEXT

Two ten-frames are shown above a student work sample. The top ten-frame shows the number 8. The bottom ten-frame shows the number 5.
The student work sample shows the equation 8 plus 5 equals 13. Two arrows extend below the 5 and connect to the numbers 2 and 3, which are shown within circles. Two equations are shown below this work.
The first equation reads 8 plus 2 plus 3 equals 13. The second equation reads 10 plus 3 equals 13.

The student's work provides evidence that the student integrates addition with which of the following skills?

  1. decomposing and composing numbers into place-value components
  2. applying the associative and commutative properties
  3. integrating inverse operations to confirm a solution
  4. understanding early fraction representations
Answer. Enter to expand or collapse. Answer expanded
Correct Response: A.
  1. Correct. The student decomposes "5" into "2 + 3" for the purpose of creating a unit of ten from the 8 and 2.
  2. The student does not rearrange terms or change the order for operations in any way, so the associative and commutative properties are not used in the solution.
  3. The student does not use subtraction in their solution, so they are not applying inverse operations.
  4. The problem involves adding whole numbers, and the student does not use fractional reasoning in their solution.